月齢
「正午月齢」について説明しています。
正午月齢
「正午月齢」は名前の通りその日の12時0分(正午)の月齢で1日の真ん中の月齢です。
夜中に見えるお月様の月齢は「正午月齢」からその時間差分変わっています。
月齢0とは
地球の中心から月を見て太陽との黄経差(こうけいさ)が0になる瞬間が月齢0(朔、新月)になる時です。
つまり太陽、月、地球が並ぶ瞬間です。
黄経は天球座標系(星の位置を決める座標)の一つである黄道(こうどう)座標系で使われます。
下の図は地心黄道座標のイメージ図です。
中心の地球から見て水色の円のまわりを周る「太陽」と「月」の黄経差が0となるときが月齢0の瞬間です。
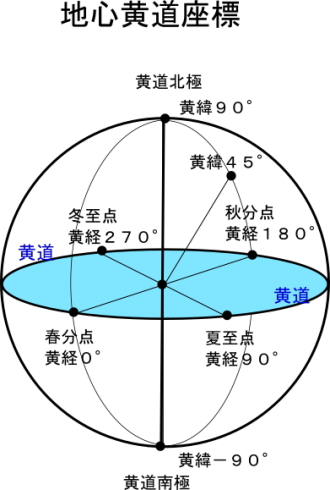
黄道座標は地球の公転軌道面を基準面として黄経、黄緯で表しています。
地球上の位置を表す緯度、経度のイメージです。
経度はグリニッジより180°ずつ東周りの東経と西周りの西経に別れていますが黄経は春分点を0°として360°で表示します。
月齢0の瞬間の黄経差は0ですが緯度を表す黄緯差(イメージ図では上下の差)は0ではなく太陽、月、地球が一直線に並ぶわけではありません。
朔(黄経差が0)になる瞬間が試算できれば、朔から正午までの時間が分るため正午月齢が計算できます。
朔になる瞬間が今日の0時0分だとすると0時0分の月齢は「0」となりますが正午月齢(12時0分)は時間差の12時間だけプラスした値になります。
1日(24時間)に1づつ増える月齢なので1×12時間/24時間=0.5をプラスして今日の正午月齢は0.5となります。
「正午月齢」が0.5と計算されたとき、次の日の「正午月齢」は1.5となり次の朔を迎えるまで毎日1づつ足されていくので小数点以下は変化せず、新しい朔になるたびにリセットされます。
望(満月)の月齢は一定でない
次の図は、小学校で習ったような気がする月の公転のイメージ図です。
新月からの黄経差が決められているのは上弦、望、下弦のみで、それぞれ黄経差が90度、180度、270度です。
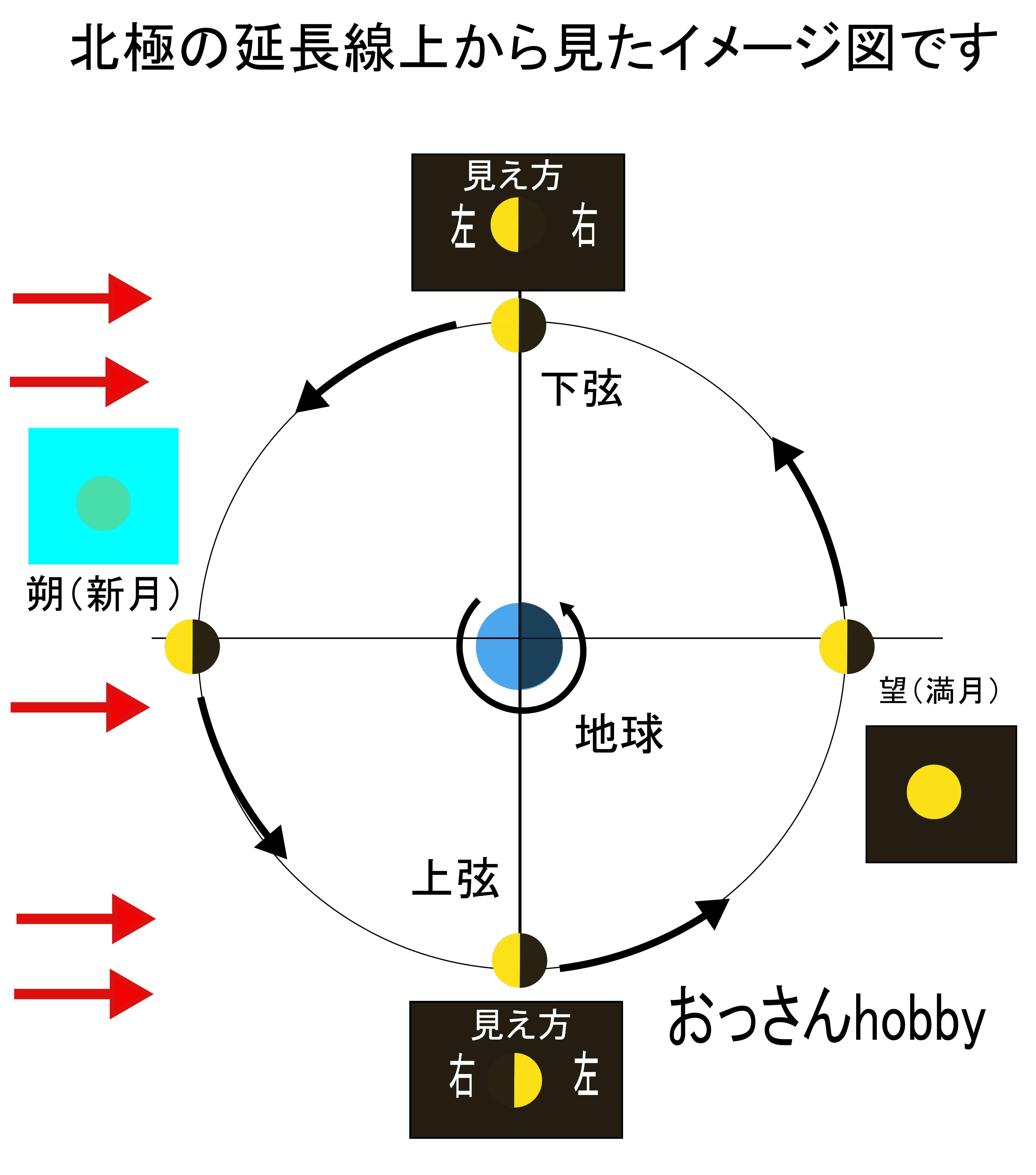
月は朔(さく:新月)から上弦(じょうげん)、望(ぼう:満月)、下弦(かげん)、朔と満ち欠けを繰り返しまが、上弦、望、下弦それぞれの月齢は様々な影響で変化するため一定していません。
いつも「日食」にはならない
黄道面と白道面(はくどう:月の公転面)が完全に重なっていれば朔を迎えるたびに地球のどこかでは日食を見ることが出来、望のたびに月食が見られるはずですが、黄道面に対し白道面は5度ほど傾いている為にその交差している付近で朔や望を迎えない限り日食、月食は起こりません。
朔望月
月の満ち欠けの周期は29.530589日で、月が地球を1周する周期は27.3216155日です。
2日以上の差には理由があります。
両者が異なる理由は30日余りかけて月が地球を公転する間に地球もひと月分、約360度÷12=30度太陽の周りを公転しているのでその分2日あまり多く回らなければ黄経差がゼロにはならないからです。
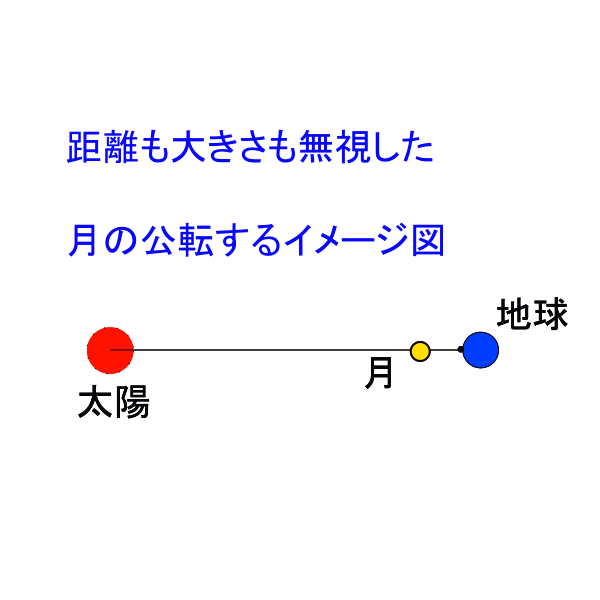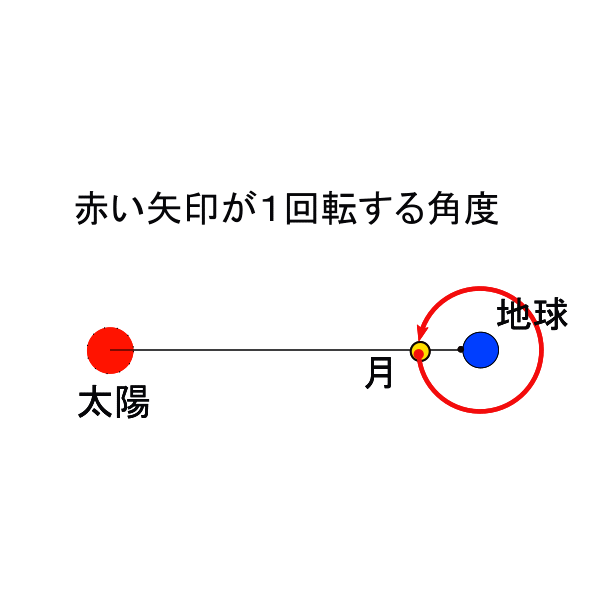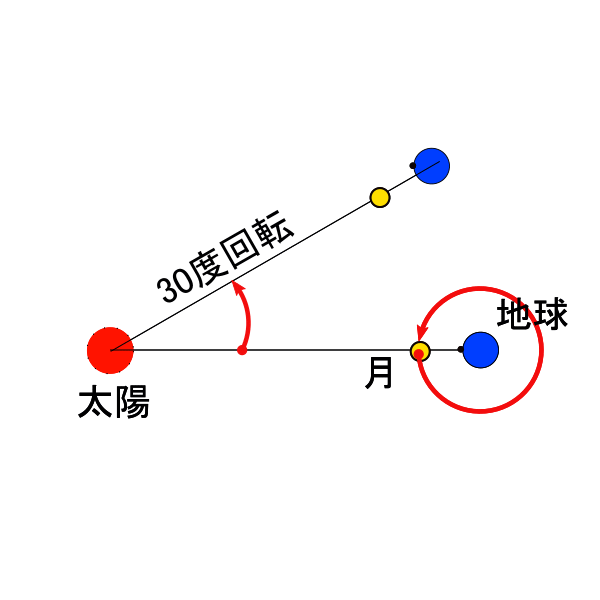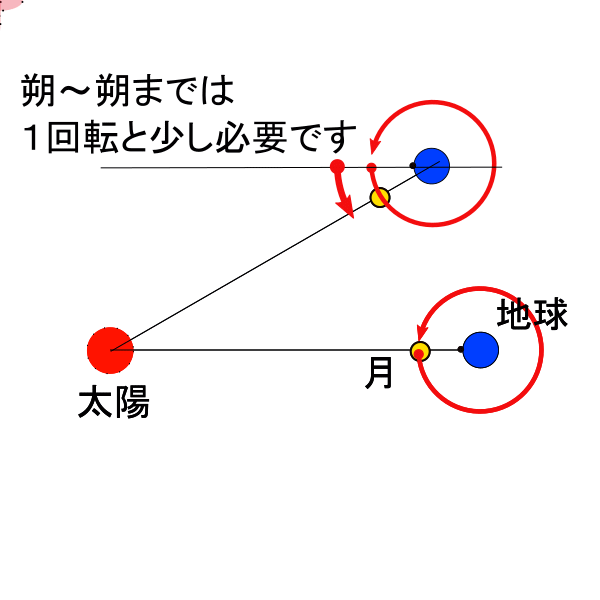
細かい話になってしまいますが、この地球と月との関係は太陽と地球の関係にも当てはまります。
地球は一日に1回転と「ちょびっと」回転(自転)しています。というより1回転とちょびっと回転するまでの間、言い換えると太陽が南中してから次に南中するまでの時間の長さを1日と決めているといったほうが正しいかもしれません。
月の1年間の軌跡は? 螺旋か波型か?
上の図を1年分つなげて太陽の周りを1周させると月の軌跡はどのようになると思いますか。
コイルばねを少し引っ張り横から見たような形? 波型? 良く分からないのでアニメーションを作り「ちょこっと」考えてみました。
次のアニメーションは見ての通り距離などは適当ですが地球の公転周期と月の公転周期は大まかに合わせています。
下のアニメーションの中の青い円で書いた地球の周りに月を示す小さな黒い点を書いています。
小さすぎて見にくいですが月を表す黒い点は、 地球が30度太陽の周りを移動する間に月は1回地球の周りを公転すると仮定して描いています。
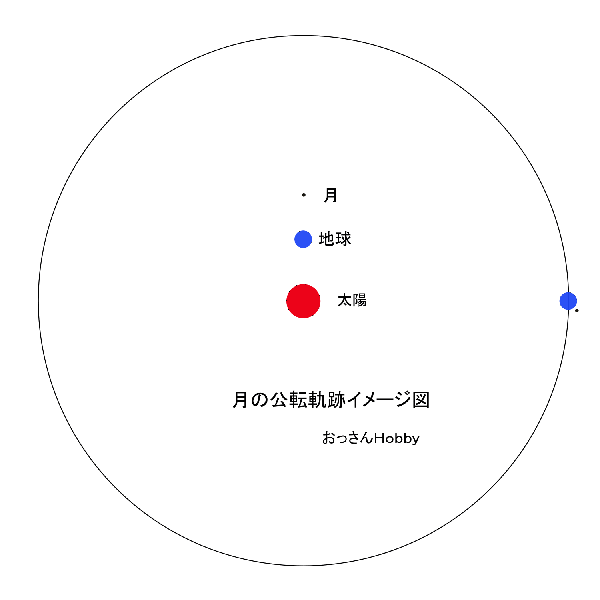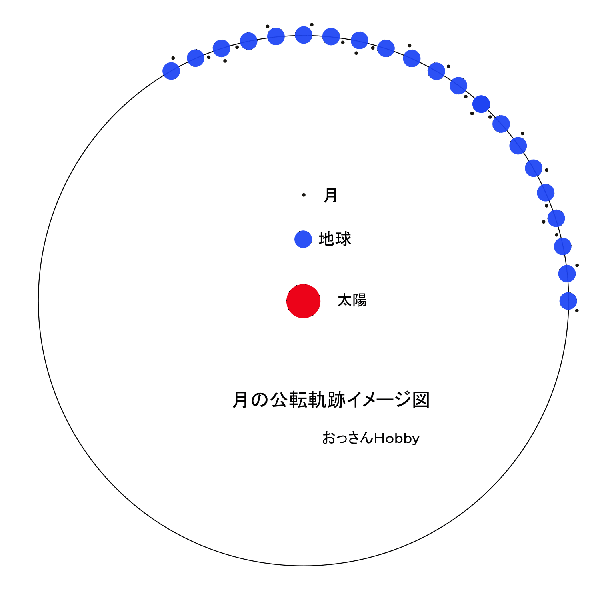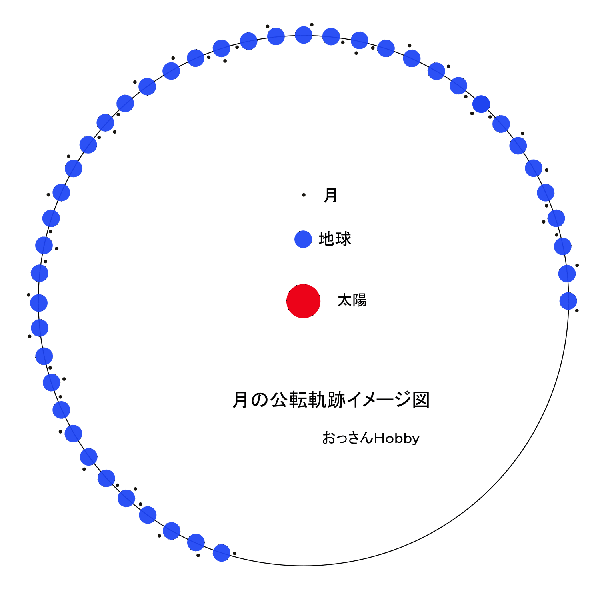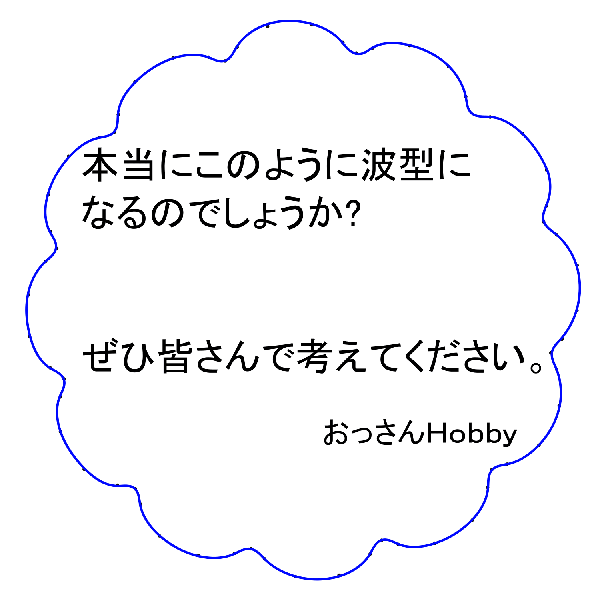
月の軌跡を線で結ぶと、あらら、波線になるようです。
てっきり螺旋状になると思っていました。
太陽と地球の距離が、149,600,000kmです。
月が地球を一周する円の直径が地球と月の距離を2倍した768,800kmです。
この数字を考えて、月の公転円を太陽から見ると角度が1度にも満たない小さな円になります。
その円が約1月かけて30度移動する間に1回転していると考えると、実際の縮尺では波型になっているのも分かりにくい円になるはずと考えましたが皆さんはどうお考えですか。
























